Ciao!

Ti sei mai chiesta/o come una persona con discalculia fa i calcoli a mente? Quali sono i pensieri e le strategie che attua, le emozioni che prova?

Oggi voglio provare a spiegarti il mio modo di fare le operazioni a mente.

Prima di cominciare, voglio specificare che, per me ha moltissima importanza se l’operazione che devo andare a fare è scritta o orale, così come il tipo di operazione.

Facciamo ora finta che, davanti a me c’è una persona e a voce mi dice

“47 + 9 quanto fa?”.

Per prima cosa ripeto nella mia testa le parole che mi sono appena state dette, più lentamente, scandendole bene, come a rallentatore.

Questo perchè, ho sentito cosa mi è stato detto, l’ho capito, ma allo stesso tempo, mi sembra essere una lingua sconosciuta e ho bisogno di una traduzione.

Conosco le parole, ma faccio fatica ad associarle al loro significato e di conseguenza capire a che simbolo corrispondono.

Nel mentre che ripeto le parole nella mia testa, posso anche mimarle con le labbra, molte volte mi è utile per dimezzare i tempi di traduzione e associazione.

Impiego circa dai 3 ai 5 secondi, dipende dalla parola.

Una volta “decifrata” la parola, la ripeto per l’ultima volta, anche questa volta la scompongo, disegnandola poi nella mia testa.

Questo è circa quello che avviene nella mia testa:

Quarantasette = ?

Qua.. = ? = 4

Quaranta.. = ? = 40

sette = ? = 7

Quarantasette = ? = 47

Schematizzando i processi diventano circa così:

ascolto -> percezione del suono -> ripetizione del suono -> scomposizione del suono con ripetizione -> traduzione del suono alla parola corrispondente -> traduzione della parola al simbolo corrispondente -> trascrizione del simbolo

La stessa cosa avviene per il 9.

Alla fine della traduzione e trascrizione del 9, dimentico cosa c’era prima, ricordo però le parole che avevo ascoltato, le ripeto un’altra volta nella mia testa, riuscendo subito ad associarle al simbolo corrispondente.

Ora nella mia testa, è come se ci fosse un foglio/lavagana, con su scritto l’operazione.

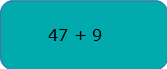
Ora, provo a raggruppare le unità con unità e decine con decine.

Le decine, per me, vanno a destra mentre le unità a sinistra.

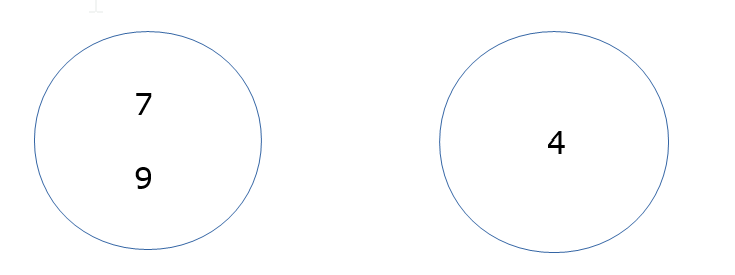
So, che sarebbe il contrario, ma il mio cervello è come se dicesse “NO!” e li vuole vedere così. E’ come se dicesse, in colonna fai prima le unità e poi le decine e quindi anche nelle bolle li devi riordinare così!

Cerco allora di fare 7 + 9, ma, essendo per me due numeri “antipatici”, sono costretta a scomporli. Per sapere come scomporli devo prima pensare alla loro rappresentazione sulle mani.

So che, per fare il 7 ci vuole una mano + due dita (5+2). Per il 9 invece, una mano + quattro dita (5+4).

Ora, ragruppo i valori uguali, 5 e 5 e li sommo (sempre pensando alle mani).

5 + 5 = una mano + una mano = 10

Successivamente faccio, 4 + 2 = 2 dita + 2 dita = una mano – 1 dito = 2 + 2 + 2 = 6.

In fine faccio, 10 + 6 = 16.

Non ho bisogno ci contare o guardare le mani, le dita per me necessarie sono immaginarie. Per svolgere tutti questi passaggi mi basta pochissimo tempo, qualche secondo, ma ho bisogno di moltissima concentrazione e tante energie, perchè ogni volta che svolgo un passaggio, rischio di dimenticare quello prima, quindi devo ripetere tutto ciò che ho fatto fino ad ora, con i relativi passaggi.

Decido ora di ripetere nuovamente l’operazione, 47 + 9, questa volta la immagino in colonna e inserisco il risultato ottenuto poco prima.

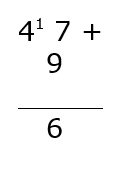
Adesso so che, il 16 è composto da 6 unità e 1 decina. 1 decina va con il 4, ovvero così:

Faccio così, 4 + 1 = una mano – 1 = 4 dita + 1 dito = 5 dita = una mano

Ripeto velocemente tutti i numeri che ho incontrato fino ad ora.

Rifaccio 7 + 9, questa volta senza fare i passaggi delle dita, faccio direttamente 5 + 2 + 5 + 4 = (5 + 5) + (2+4) = 10 + 6 = 16

Immagino nuovamente tutto in colonna:

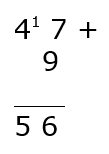
Il risultato della mia operazione è 56.

Tutti questi passaggi avvengono, appunto, più volte nella mia testa, perchè dimentico e devo ricominciare da capo. Avvengono molto velocemente.

In media, per un operazione a mente, simile a questa, impiego 8 secondi.